Fonctions récursives

Vous avez sans doute remarqué que jusqu’à présent, nous n’avions pas utilisé de boucles for, while ou autre. Et en effet, les langages fonctionnels ne proposent pas ce genre de structures. Pour répéter plusieurs fois une même opération, on va plutôt utiliser des fonctions récursives.

La définition est très simple : c’est juste une fonction qui s’appelle elle-même à un moment donné. De manière générale, ces fonctions définissent deux cas de figure (avec un if/else ou un match) : un cas de base qui ne récurse pas, et un cas récursif qui appelle la fonction récursivement au « rang » d’avant.

Oublier le cas de base aura le même effet qu’un while(True) en Python : la fonction ne cessera jamais de s’appeler et votre programme tournera à l’infini.

En OCaml, il faudra utiliser le mot-clé rec après let pour préciser qu’une fonction est récursive.

Voici un exemple de fonction qui calcule récursivement la somme des éléments de 0 à n :

(* On considère que n n’est pas négatif même si le type int l’autorise *)
let rec somme (n : int) : int =
  if n = 0 then
    0
  else
    n + (somme (n - 1))

Ici :

• le cas de base est 0 pour n = 0 ;
• le cas récursif est n + (somme (n - 1)) sinon.

Pour comprendre comment cette fonction marche pour n = 3, on peut utiliser le schéma suivant :

Ou alternativement, celui-ci :

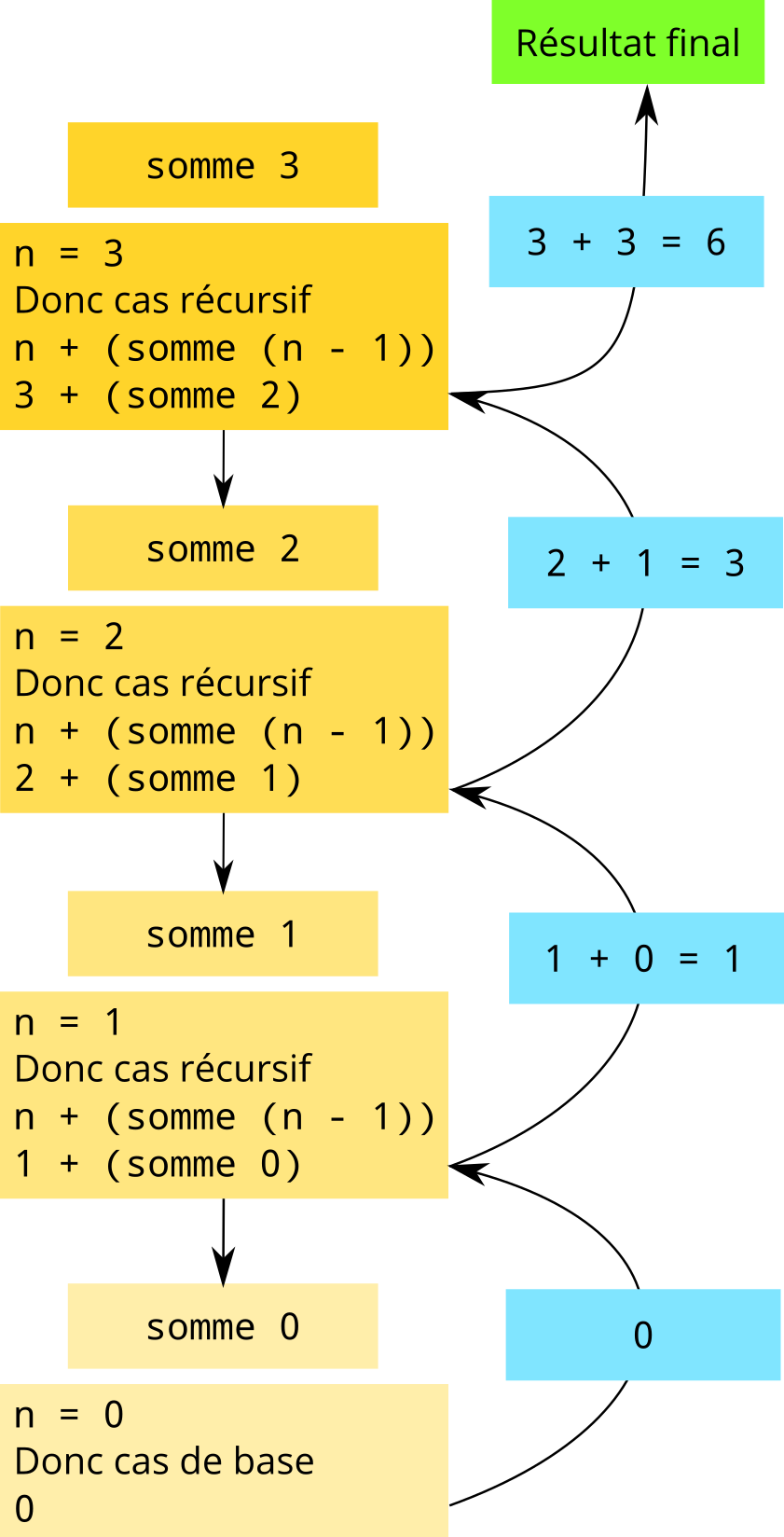
Utilisez celui que vous préférez, l’important est d’arriver à comprendre comment cette fonction fait ce calcul (utilisez les deux si vous voulez même). Une fois que vous aurez saisi le principe de base, vous comprendrez assez facilement toutes les fonctions récursives. Il faut juste avoir le déclic. Si vous voulez, voici quelques autres exemples de fonctions récursives :

let rec factorielle n =
  if n < 2 then
    1
  else
    n * (factorielle (n - 1))

(* Si vous ne savez pas ce qu’est la suite de Fibonacci : https://fr.wikipedia.org/wiki/Suite_de_Fibonacci *)
let rec fibonacci n =
  if n < 2 then
    1
  else
    (fibonacci (n - 1)) + (fibonacci (n - 2))

Une analogie qui peut aussi aider à comprendre est la notion de suite récursive : pour calculer u(n), on a toujours besoin de u(n - 1), et on doit donc tous les calculer jusqu’à atteindre u(0) qui est défini de manière constante (le cas de base).

Les fonctions récursives peuvent servir à faire tout ce que font les boucles dans d’autres langages de programmation, et plus encore. Certains algorithmes de tri peuvent être implémentés récursivement, et certaines fonctions sont même impossible à écrire autrement. En OCaml (et dans beaucoup d’autres langages fonctionnels), la récursivité est en permanence utilisée pour manipuler les listes. C’est donc un outil très puissant, mais il faut prendre le temps de bien le comprendre.